Consider a probability density \(\pi(x)\) on \(\mathbb{R}^d\) and a (deterministic) function \(F: \mathbb{R}^d \to \mathbb{R}^d\). Assume further that \(F\) is an involution in the sense that
\[ F(F(x)) = x \]
for all \(x \in \mathbb{R}^d\). To keep things simple since it is not really the point of this short note, suppose that \(\pi(x)>0\) everywhere and that \(F\) is smooth. This type of transformations can be used to define Markov Chain Monte Carlo algorithms, eg. the standard Hamiltonian Monte Carlo (HMC) algorithm. To design a MCMC scheme with this involution \(F\), one needs to answer the following basic question: suppose that \(X \sim \pi(dx)\) and the proposal \(Y = F(X)\) is constructed and accepted with probability \(\alpha(X)\), how should the acceptance probability function \(\alpha: \mathbb{R}^d \to [0,1]\) be chosen so that the resulting random variable \[Z \; = \; Y \, B + (1-B) \, X\] is also distributed according to \(\pi(dx)\)? The Bernoulli random variable \(B\) is such that \(\mathbb{P}(B=1|X=x)=\alpha(x)\). In other words, for any test function \(\varphi: \mathbb{R}^d \to \mathbb{R}\), we would like \(\mathbb{E}[\varphi(Z)] = \mathbb{E}[\varphi(X)]\), which means that
\[ \int {\left\{ \varphi(F(x)) \, \alpha(x) + \varphi(x) \, (1-\alpha(x)) \right\}} \, \pi(dx) = \int \varphi(x) \, \pi(dx). \tag{1}\]
Requiring for Equation 1 to hold for any test function \(\varphi\) is easily seen to be equivalent to asking for the equation
\[ \alpha(x) \, \pi(x) \; = \; \alpha(y) \, \pi(y) \, |J_F(x)| \]
to hold for any \(x \in \mathbb{R}^d\) where \(y=F(x)\) and \(J_F(x)\) is the Jacobian of \(F\) at \(x\). Since \(|J_F(y)| \times |J_F(x)| = 1\) because the function \(F\) is an involution, this also reads
\[ \alpha(x) \, \frac{\pi(x) }{|J_F(x)|^{1/2}} \; = \; \alpha(y) \, \frac{\pi(y) }{|J_F(y)|^{1/2}}. \]
At this point, it becomes clear to anyone familiar with the the correctness-proof of the usual Metropolis-Hastings algorithm that a possible solution is
\[ \alpha(x) \; = \; \min {\left\{ 1, \frac{\pi(y) / |J_F(y)|^{1/2}}{\pi(x) / |J_F(x)|^{1/2}} \right\}} \]
although there are indeed many other possible solutions. Since \(|J_F(y)| \times |J_F(x)| = 1\), this also reads
\[ \alpha(x) \; = \; \min {\left\{ 1, \frac{\pi(y)}{\pi(x)} \, |J_F(x)| \right\}} . \tag{2}\]
One can reach a similar conclusion by looking at the Radon-Nikodym ratio \([\pi(dx) \otimes q(x,dy)] / [\pi(dy) \otimes q(y,dx)]\) where \(q(x,dy)\) is the markov kernel described the deterministic transformation (Green 1995), but I do not find this approach significantly simpler. The very neat article (Andrieu, Lee, and Livingstone 2020) describes much more sophisticated and interesting generalizations. Indeed, Equation 2 is often used in the simpler case when \(F\) is volume preserving, i.e. \(|J_F(x)|=1\), as is the case for the Hamiltonian Monte Carlo (HMC). The discussion above was prompted by a student implementing a variant of this but with the wrong acceptance ratio \(\alpha(x) = \min {\left\{ 1, \frac{\pi(y)}{\pi(x)} \, \frac{|J_F(x)|}{|J_F(y)|} \right\}} \) and us taking quite a bit of time to find the bug…
Note that there are interesting and practical situations when the function \(F\) satisfies the involution property \(F(F(x))=x\) only when \(x\) belongs to a subset of the state-space. For instance, this can happen when implementing MCMC on a manifold \(\mathcal{M} \subset \mathbb{R}^d\) and the function \(F\) involves a “projection” on the manifold \(\mathcal{M}\), as for example described in the really interesting article (Zappa, Holmes-Cerfon, and Goodman 2018). In that case, it suffices to add a “reversibility check”, i.e. make sure that when applying \(F\) to the proposal \(y=F(x)\), one goes back to \(x\) in the sense that \(F(y)=x\). The acceptance probability in that case should be amended and expressed as
\[ \alpha(x) \; = \; \min {\left\{ 1, \frac{\pi(y)}{\pi(x)} \, |J_F(x)| \right\}} \, \mathbf{1} {\left( F(y)=x \right)} . \]
In other words, if applying \(F\) to the proposal \(y=F(x)\) does not lead back to \(x\), the proposal is always rejected.
Same, but without involution
in some situations, the requirement for \(F\) to be an involution can seem cumbersome. What if we consider the more general situation of a smooth bijection \(T: \mathbb{R}^d \to \mathbb{R}^d\) and its inverse \(T^{-1}\)? In that case, one can directly apply what has been described in the previous section: it suffices to consider an extended state-space \((x,\varepsilon)\) obtained by including an index \(\varepsilon\in \{-1,1\}\) and the involution \(F\) defined as
\[ F: \left\{ \begin{align} (x,\varepsilon=+1) &\mapsto (T(x), \varepsilon=-1)\\ (x,\varepsilon=-1) &\mapsto (T^{-1}(x), \varepsilon=+1). \end{align} \right. \tag{3}\]
This allows one to define a Markov kernel that lets the distribution \(\overline{\pi}(x, \varepsilon) = \pi(dx)/2\) invariant. Things can even start to get a bit more interesting if a deterministic “flip” \((x, \varepsilon) \mapsto (x, -\varepsilon)\) is applied after each application of the Markov kernel above describe: doing so avoids immediately coming back to \(x\) in the event the move \((x,\varepsilon) \mapsto (T^{\varepsilon}(x), -\varepsilon)\) is accepted. There are indeed quite a few papers exploiting this type of ideas.
A mixture of deterministic transformations?
To conclude these notes, here is a small riddle whose answer I do not have. One can check that for any \(c \in \mathbb{R}\), the function \(F_{c}(x) = c + 1/(x-c)\) is an involution of the real line. This means that for any target density \(\pi(x)\) on the real line, one can build the associated Markov kernel \(M_c\) defined as
\[ M_c(x, dy) = \alpha_c(x) \, \delta_{F_c(x)}(dy) + (1-\alpha_c(x)) \, \delta_x(dy) \]
for an acceptance probability \(\alpha_c(x)\) described as above,
\[ \alpha_c(x) = \min {\left\{ 1, \frac{\pi[F_c(x)]}{\pi(x)} |F'_c(x)| \right\}} . \]
Finally, choose a \(N \geq 2\) values \(c_1, \ldots, c_N \in \mathbb{R}\) and consider the mixture of Markov kernels
\[ M(x,dy) \; = \; \frac{1}{N} \sum_{i=1}^N M_{c_i}(x, dy). \]
The Markov kernel \(M(x, dy)\) lets the distribution \(\pi\) invariant since each Markov kernel \(M_{c_i}(x, dy)\) does, but it is not clear at all (to me) under what conditions the associated MCMC algorithm does converge to \(\pi\). One can empirically check that if \(N\) is very small, things can break down quite easily. On the other, for \(N\) large, the mixuture of Markov kernels \(M(x,dy)\) empirically seems to behave as if it were ergodic with respect to \(\pi\).
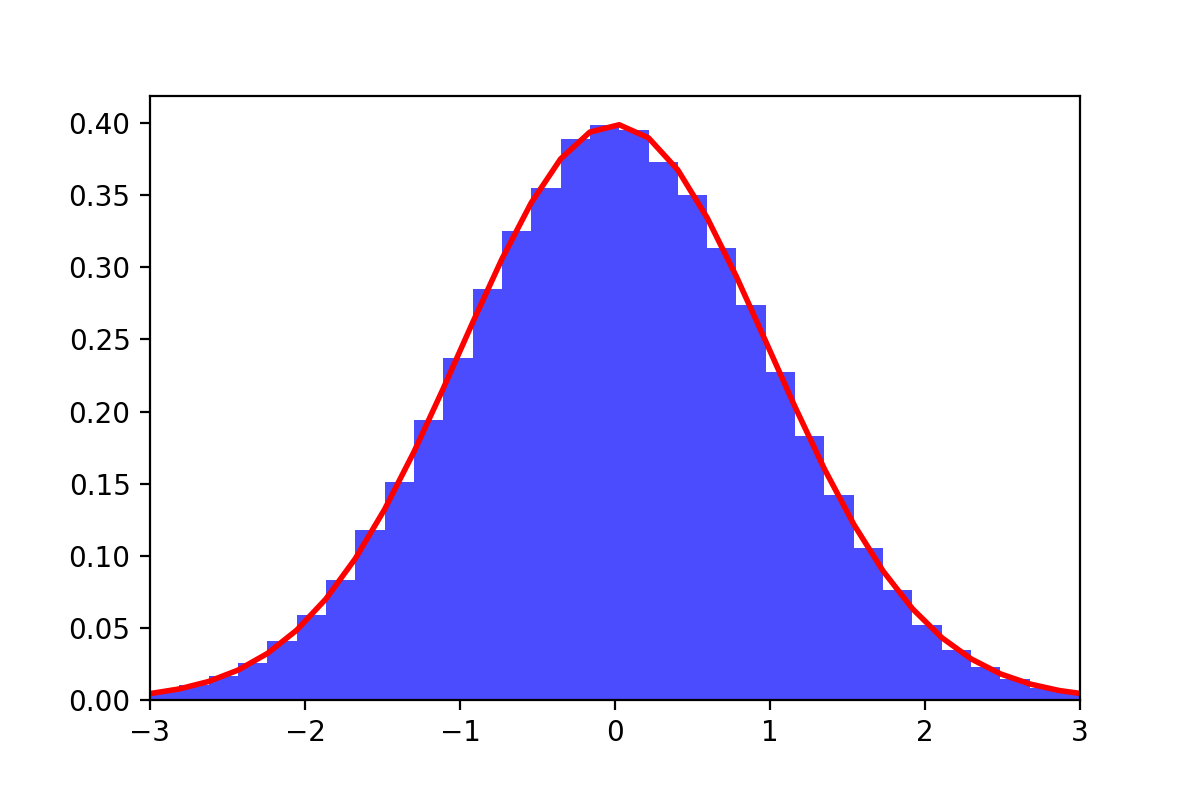
For \(N=5\) values \(c_1, \ldots, c_5 \in \mathbb{R}\) chosen at random, the illustration aboves shows the empirical distribution of the associated Markov chain ran for \(T=10^6\) iterations and targeting the standard Gaussian distribution \(\pi(dx) \equiv \mathcal{N}(0,1)\): the fit seems almost perfect.