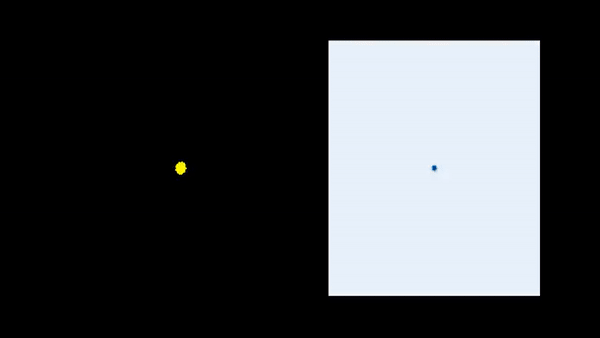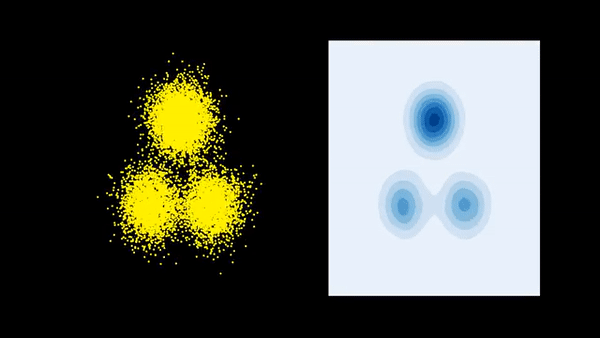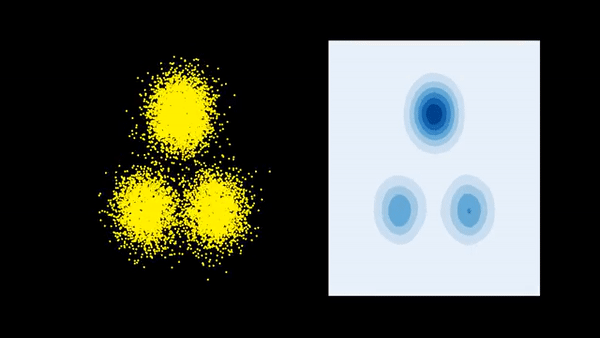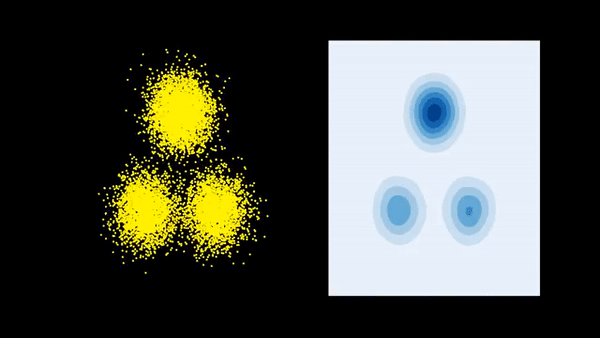
Consider a target probability density \(\pi(x) = \frac{\overline{\pi}(x)}{\mathcal{Z}}\) on \(\mathbb{R}^D\) that is known up to a normalizing constant \(\mathcal{Z}> 0\). We also have a different probability density \(p_0(x)\). The goal is to gradually tweak \(p_0(x)\) so that it eventually matches \(\pi(x)\). More concretely, we aim to perform a gradient descent on the space of probability distributions to reduce the functional
\[ \mathcal{F}(p) \; = \; D_{\text{KL}} {\left( p, \pi \right)} \; = \; \int p(x) \, \log {\left\{ \frac{p(x)}{\overline{\pi}(x)} \right\}} \, dx \, + \, \textrm{(constant)}. \]
This approach can be discretized: assume \(N \gg 1\) particles \(X_0^1, \ldots, X_0^N \in \mathbb{R}^D\) forming an empirical distribution that approximates \(p_0(dx)\),
\[ p_0(dx) \; \approx \; \frac{1}{N} \sum_{i=1}^N \, \delta_{X_0^i}(dx). \]
Define \(X_{\delta}^i = X_0^i + \delta_t \, \mu(X_0^i)\) where \(\delta_t \ll 1\) denotes a time discretization parameter and \(\mu:\mathbb{R}^D \to \mathbb{R}^D\) is a “drift” function. Finding a suitable ‘drift function’ is the main problem. According to the Fokker-Planck equation, the computed empirical distribution
\[ p_{\delta_t}(dx) \; \approx \; \frac{1}{N} \sum_{i=1}^N \, \delta_{X_{\delta_t}^i}(dx) \]
approximates \(p_{\delta_t}(x)\) given by
\[ \frac{p_{\delta_t}(x)- p_0(x)}{\delta_t} \; = \; -\nabla \cdot {\left[ \mu(x) \, p_0(x) \right]} . \tag{1}\]
What is the optimal drift function \(\mu: \mathbb{R}^D \to \mathbb{R}^D\) that ensures that \(p_{\delta_t}\) comes as close as possible to \(\pi\)? Typically, we select \(\mu:\mathbb{R}^D \to \mathbb{R}^D\) such that the quantity \(\mathcal{F}(p_{\delta_t})\) is minimized, provided that \(p_{\delta_t}\) is not drastically different from \(p_0\). One method is to use the \(L^2\) Wasserstein distance and assume the constraint
\[ D_{\text{Wass}}(p_{0}, p_{\delta_t}) \approx \int p_0(x) \, \| \delta_t \, \mu(x) \|^2 \, dx \leq \varepsilon \tag{2}\]
for a parameter \(\varepsilon\ll 1\). More pragmatically, it is generally easier (eg. proximal methods) to minimize the joint objective
\[ \mathcal{F}(p_{\delta_t}) + \frac{1}{2 \varepsilon} \, D_{\text{Wass}}(p_{0}, p_{\delta_t}). \tag{3}\]
Based on equations Equation 1 and Equation 2, a first-order expansion shows that the joint objective Equation 3 can be approximated by
\[ % \begin{align} \begin{multline} -\int \nabla \cdot \Big\{ \textcolor{red}{[\delta_t \mu]}(x) \, p_0(x) \Big\} \, \log {\left\{ \frac{p_0(x)}{\overline{\pi}(x)} \right\}} \, dx \, \\ \frac{1}{2 \varepsilon} \, \int p_0(x) \, \| \textcolor{red}{[\delta_t \, \mu]}(x) \|^2 \, dx. \end{multline} % \end{align} \tag{4}\]
Adopting the usual scaling \(\varepsilon= \delta_t\), we can minimize pointwise in \(x\) to obtain the optimal drift function: \[ \mu(x) \; = \; - \nabla \log {\left\{ \frac{p_0(x)}{\overline{\pi}(x) } \right\}} . \]
Put simply, this suggests that we should select the drift function proportional to \(-\nabla \log[p_0(x) / \overline{\pi}(x)]\). To implement this scheme, we begin by sampling \(N \gg 1\) particles \(X_0^i \sim p_0(dx)\) and let evolve each particle according to the following differential equation
\[ \frac{d}{dt} X_t^i \; = \; - \nabla \log {\left\{ \frac{p_t(X_t^i) }{ \overline{\pi}(X_t^i) } \right\}} \]
where \(p_t\) is the density of the set of particles at time \(t\). It is the usual diffusion-ODE trick for describing the evolution of the density of an overdamped Langevin diffusion,
\[ dX_t \; = \; \nabla \log \overline{\pi}(X_t) \, dt \; + \; \sqrt{2} \, dW_t. \]
This can be shown by writing down the associated Fokker-Planck equation. This heuristic discussion shows that minimizing \(D_{\text{KL}}(p, \pi)\) by introducing a gradient flow in the space of probability distributions with the Wasserstein metric essentially produces a standard overdamped Langevin diffusion. Indeed, transforming this heuristic discussion into a formal statement is not trivial: the constructive proof in (Jordan, Kinderlehrer, and Otto 1998) is now usually referred to as the JKO scheme.
The above derivation shows that the Wasserstein distance plays particularly well with minimizing functionals of the space of probability distributions. Naturally, one may wonder what happens when considering other functionals \(\mathcal{F}(p)\).
A More General Functional \(\mathcal{F}(p)\)
In the previous section, we focused on the specific objective \(\mathcal{F}(p) = D_{\text{KL}}(p,\pi)\) and derived the associated Wasserstein gradient flow. The key step was to compute how the KL functional reacted to perturbations of the density \(p\) when mass was rearranged according to a vector field \(\mu:\mathbb{R}^D \to \mathbb{R}^D\). Essentially the same reasoning applies to a wide class of functionals \(\mathcal{F}\) defined on probability distributions. Assume that \(\mathcal{F}(p)\) admits a functional derivative, written \(\frac{\delta \mathcal{F}}{\delta p}(x)\); this means that for any perturbation of the density \(p\) of the form \(p + \varepsilon q\) where \(q\) is a signed-measure of total mass zero and \(\varepsilon\ll 1\), we have the expansion:
\[ \mathcal{F}(p + \varepsilon q) = \mathcal{F}(p) \;+\; \varepsilon \int \textcolor{blue}{\frac{\delta \mathcal{F}}{\delta p}(x) }\, q(dx) \;+\; o(\varepsilon). \tag{5}\]
Here, the term \( \textcolor{blue}{\delta \mathcal{F}/ \delta p}\) is just a standard function from \(\mathbb{R}^D\) to \(\mathbb{R}\) and several examples are given below. If we perturb the current distribution \(p_0\) by transporting it along a vector field \(\mu:\mathbb{R}^D\to\mathbb{R}^D\) during a time interval of length \(\delta_t \ll 1\), the continuity equation gives: \[ p_{\delta_t}(x) = p_0(x) \;-\; \delta_t\, \nabla\cdot {\left( p_0(x)\,\mu(x) \right)} \;+\; O(\delta_t^2). \]
Using definition Equation 5, we can compute the resulting change in \(\mathcal{F}\):
\[ \begin{align*} \mathcal{F}(p_{\delta_t}) - \mathcal{F}(p_0) &\approx - \delta_t \int \frac{\delta \mathcal{F}}{\delta p}(x)\, \nabla\cdot\{ p_0(x)\,\mu(x) \} \, dx\\ &= \delta_t \int p_0(x)\, \mu(x)\cdot \nabla\!\left[ \frac{\delta \mathcal{F}}{\delta p}(x) \right] dx. \end{align*} \]
We have assumed sufficient regularity to perform an integration by parts and neglect boundary terms. This identity describes how the functional reacts when mass is rearranged according to the vector field \(\mu\). It is the direct analogue of the KL computation earlier in the note, but now valid for any functional \(\mathcal{F}\) admitting a functional derivative. We can then proceed as before to find the optimal drift \(\mu\) under a Wasserstein penalty. We would like to minimize the proximal objective: \[ \mathcal{J}(\mu) = \mathcal{F}(p_{\delta_t}) \;+\; \frac{1}{2\varepsilon}\, D_{\text{Wass}}(p_0,p_{\delta_t})^2 \]
where \(\varepsilon\ll 1\) is a scaling parameter that can be thought of as a step-size. Since \(D_{\text{Wass}}(p_0, p_{\delta_t})^2 \approx \delta_t^2 \int p_0(x)\, \|\mu(x)\|^2\, dx\) to leading order, the proximal objective can be approximated as a simple quadratic functional of the vector field \(\mu\). Minimizing pointwise in \(x\) and adopting the usual scaling \(\varepsilon= \delta_t\) gives the optimal velocity field, i.e. the negative Wasserstein gradient of \(\mathcal{F}\) reads: \[ \textcolor{blue}{\mu(x) = - \nabla\!\left[ \frac{\delta \mathcal{F}}{\delta p}(x) \right].} \]
Inserting the optimal drift into the continuity equation yields the Wasserstein gradient flow for minimizing the functional \(\mathcal{F}\): \[ \partial_t p_t(x) = \nabla\cdot \Big( p_t(x)\, \nabla\!\left[ \frac{\delta \mathcal{F}}{\delta p_t}(x) \right] \Big). \]
This partial differential equation describes how the density (or empirical measure) evolves when we follow the direction of steepest descent of \(\mathcal{F}\) with respect to the Wasserstein metric. A few common choices of \(\mathcal{F}\) illustrate the general formula:
Entropy:
The functional \(\mathcal{F}_{\textrm{ent}}(p) = -\int p(x)\log p(x)\,dx\) has derivative \(\frac{\delta \mathcal{F}_{\textrm{ent}}}{\delta p} = -(\log p + 1)\). This means that the Wasserstein gradient flow to maximize the entropy is given by the heat equation: \[ \partial_t p_t(x) = \nabla \cdot {\left( p_t(x) \, \nabla \log p_t(x) \right)} = \Delta p_t(x). \] This describes the evolution of the density of a standard Brownian motion, i.e. particles moving according to the SDE:
\[dX_t = \sqrt{2}\,dW_t.\]
External potential
Now, consider a potential function \(V:\mathbb{R}^D \to \mathbb{R}\) and the functional \(\mathcal{F}(p) = \int V(x)\,p(x)\, dx\). The functional derivative is simply \(\frac{\delta \mathcal{F}}{\delta p}(x) = V(x)\), so the Wasserstein gradient flow to minimize the potential energy is \[ \partial_t p_t = \nabla\cdot \Big( p_t \,\nabla V \Big). \] This describes the evolution of the density of particles doing steepest descent in the potential \(V\), i.e. particles moving according to the ODE:
\[dX_t = -\nabla V(X_t)\,dt\]
as is very intuitive. When combined with the entropy functional, i.e. when minimizing the functional
\[\mathcal{F}(p) = \int V(x)\,p(x)\, dx - \mathcal{F}_{\textrm{ent}}(p),\]
this recovers the full overdamped Langevin dynamics, i.e. particles moving according to the SDE:
\[dX_t = -\nabla V(X_t)\,dt + \sqrt{2}\,dW_t\]
as described earlier.
Forward KL:
For a target density \(\pi(x)\) consider the functional
\[\mathcal{F}(p) = D_{\text{KL}}(\pi, p) = -\int \pi(x)\, \log p(x)\, dx + \textrm{(constant)}.\]
The functional derivative is \(\frac{\delta \mathcal{F}}{\delta p}(x) = -\frac{\pi(x)}{p(x)}\), so the Wasserstein gradient flow reads: \[ \partial_t p_t = -\nabla\cdot \Big( p_t(x) \,\nabla {\left\{ \frac{\pi(x)}{p_t(x)} \right\}} \Big). \]
This cannot be interpreted as the evolution of the density of a standard diffusion process since the vector field depends on the density itself in a non-linear way. This is in contrast with the previous examples where the vector field depended only on the position \(x\).
Mean-field interaction:
Consider a symmetric interaction potential \(W:\mathbb{R}^D \to \mathbb{R}\) and the following functional: \[\mathcal{F}(p) = \frac{1}{2}\iint W(x,y) p(x)p(y)\,dx\,dy = \frac12 \, \int {\left[ W \star p \right]} (x) \, p(x)\, dx\] where we have defined the operation \( {\left[ W \star p \right]} (x) = \int W(x,y)\, p(y)\, dy\) as the interaction potential at location \(x\) induced by the density \(p\). This functional describes pairwise interactions between particles according to the potential \(W\). The functional derivative can be computed as
\[ \frac{\delta \mathcal{F}}{\delta p}(x) = \int W(x,y)\, p(y) \, dy = [W \star p](x). \]
In the case when \(W(x,y) = W(x - y)\) is translation invariant, the functional derivative is the standard convolution operation between \(W\) and \(p\). The resulting PDE for the density evolution is;
\[ \partial_t p_t = \nabla\cdot \Big( p_t\,\nabla \big[ W \star p_t \big] \Big) = \nabla \cdot \Big( p_t(x) \, \int \nabla_x W(x,y) \, p_t(y) \, dy \Big). \]
If one defines the vector field:
\[ \mu_t(p_t, x) = -\int \nabla_x W(x,y) \, p_t(y) \, dy, \]
the Wasserstein gradient flow describes the evolution of the density of particles moving according to the mean-field interaction ODE: \(dX_t = \mu_t(p_t, X_t)\,dt\). Contrary to the previous examples, this is not a standard diffusion process since the vector field \(\mu_t\) depends on the distribution of the particles itself. Such processes are usually referred to as McKean-Vlasov or mean-field processes. It is instructive to consider the special case of a quadratic interaction potential \(W(x,y) = \|x - y\|^2\). When evolving within this potential, the particle are attracted to each other. When taking into account all the pairwise interactions, this means that each particle should be attracted to the mean of the distribution, as a short computation shows: since \(\nabla_x W(x,y) = 2(x - y)\), each particle moves according to the ODE:
\[ dX_t = -2 \, {\left( X_t - \textcolor{blue}{m_t} \right)} \, dt \]
where \( \textcolor{blue}{m_t = \int x \, p_t(x) \, dx}\) denotes the mean of the distribution at time \(t\). This also shows that the mean of the distribution remains constant through time, i.e. \(dm_t/dt = 0\), and eventually all particles collapse to the initial mean as \(t \to \infty\). We have: \(X_t = \textcolor{blue}{m_0} + e^{-2t} (X_0 - \textcolor{blue}{m})\), so nothing really interesting… It becomes more interesting when combining this interaction potential with an external potential and entropy!